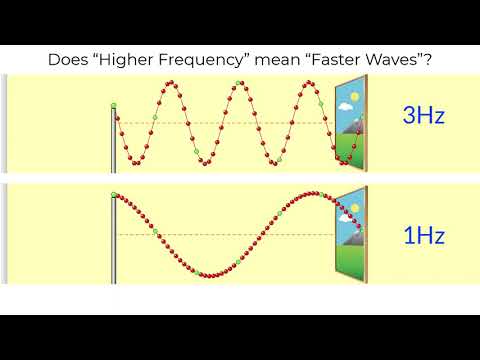
तरंग दैर्ध्य बनाम आवृत्ति
तरंग यांत्रिकी में आवृत्ति और तरंग दैर्ध्य दो घटनाएं हैं। एक दोलन की आवृत्ति बताती है कि घटना कितनी "अक्सर" होती है। एक तरंग की तरंग दैर्ध्य एक इकाई तरंग की लंबाई का वर्णन करती है। तरंग यांत्रिकी, आधुनिक भौतिकी, क्वांटम यांत्रिकी और विद्युत चुम्बकीय क्षेत्र सिद्धांत जैसे क्षेत्रों को समझने में ये दोनों अवधारणाएँ बहुत महत्वपूर्ण हैं। ऐसे क्षेत्रों में उत्कृष्टता प्राप्त करने के लिए इन अवधारणाओं की स्पष्ट समझ होना महत्वपूर्ण है। इस लेख में, हम चर्चा करने जा रहे हैं कि आवृत्ति और तरंग दैर्ध्य क्या हैं, उनकी परिभाषाएं, तरंग दैर्ध्य और आवृत्ति की समानताएं और अंत में तरंग दैर्ध्य और आवृत्ति के बीच का अंतर।
आवृत्ति
आवृत्ति एक अवधारणा है जिसकी चर्चा वस्तुओं की आवधिक गतियों में की जाती है। आवृत्ति की अवधारणा को समझने के लिए, आवधिक गतियों की उचित समझ आवश्यक है। एक आवधिक गति को किसी भी गति के रूप में माना जा सकता है जो एक निश्चित समय अवधि में खुद को दोहराता है। सूर्य के चारों ओर चक्कर लगाने वाला ग्रह एक आवर्त गति है। पृथ्वी के चारों ओर परिक्रमा करने वाला एक उपग्रह एक आवधिक गति है; यहां तक कि एक बैलेंस बॉल सेट की गति भी एक आवधिक गति है। हमारे सामने आने वाली अधिकांश आवधिक गतियाँ वृत्ताकार, रैखिक या अर्धवृत्ताकार होती हैं। आवधिक गति की एक आवृत्ति होती है। आवृत्ति का अर्थ है कि घटना कितनी "अक्सर" होती है। सरलता के लिए, हम आवृत्ति को प्रति सेकंड घटनाओं के रूप में लेते हैं। आवधिक गति या तो एकसमान या गैर-समान हो सकती है। एक वर्दी में एक समान कोणीय वेग हो सकता है। आयाम मॉडुलन जैसे कार्यों में दोहरी अवधि हो सकती है। वे अन्य आवधिक कार्यों में निहित आवधिक कार्य हैं। आवधिक गति की आवृत्ति का व्युत्क्रम एक अवधि के लिए समय देता है।सरल हार्मोनिक गति और नम हार्मोनिक गति भी आवधिक गति हैं। इस प्रकार दो समान घटनाओं के बीच समय अंतर का उपयोग करके आवधिक गति की आवृत्ति भी प्राप्त की जा सकती है। एक साधारण लोलक की आवृत्ति केवल लोलक की लंबाई और छोटे दोलनों के लिए गुरुत्वाकर्षण त्वरण पर निर्भर करती है।
तरंग दैर्ध्य
तरंगदैर्घ्य तरंगों के नीचे चर्चा की गई एक अवधारणा है। तरंग की तरंगदैर्घ्य वह लंबाई है जहां तरंग का आकार स्वयं को दोहराने लगता है। इसे तरंग समीकरण का उपयोग करके परिभाषित किया जा सकता है। एक समय पर निर्भर तरंग समीकरण ψ(x, t) के लिए, एक निश्चित समय में, यदि (x, t) दो x मानों के लिए बराबर है और समान ψ मान वाले दो बिंदुओं के बीच कोई बिंदु नहीं है, तो x का अंतर मानों को तरंग की तरंग दैर्ध्य के रूप में जाना जाता है। तरंग दैर्ध्य, आवृत्ति और तरंग के वेग के बीच संबंध v=f द्वारा दिया जाता है, जहां f तरंग की आवृत्ति है और तरंग दैर्ध्य है। किसी दी गई तरंग के लिए, चूंकि तरंग वेग स्थिर है, तरंगदैर्घ्य आवृत्ति के व्युत्क्रमानुपाती हो जाता है।
आवृत्ति और तरंग दैर्ध्य में क्या अंतर है?
• तरंगों और कंपन दोनों के लिए और किसी भी अन्य आवधिक गति के लिए आवृत्ति को परिभाषित किया जा सकता है।
• तरंगदैर्घ्य केवल एक तरंग को परिभाषित किया जाता है। आवृत्ति को हर्ट्ज़ में मापा जाता है। तरंग दैर्ध्य मीटर में मापा जाता है। तरंग की तरंग दैर्ध्य तरंग की ऊर्जा के व्युत्क्रमानुपाती होती है। आवृत्ति तरंग की ऊर्जा के रैखिक रूप से आनुपातिक होती है।